
Every machine Learning build needs to accomplish exact forecasts with their calculations. Such learning calculations are by and large divided into two sorts: directed and unsupervised. K-means clustering is one of the unsupervised calculations where the accessible input information does not have a labeled response.
What is Clustering
Clustering is like sorting a bunch of similar things into distinctive bunches based on their characteristics. In information mining and machine learning, it’s a effective method utilized to bunch comparative information focuses together, making it less demanding to discover designs or get it huge datasets. Basically, clustering helps distinguish characteristic groupings in your information. There are two common sorts of clustering methods:
Types of Clustering
Clustering is a sort of unsupervised learning wherein information focuses are assembled into diverse sets based on their degree of similarity.
The different sorts of clustering are:
Hierarchical clustering is advance subdivided into:
Partitioning clustering is encourage subdivided into:
Hierarchical Clustering
Hierarchical clustering employments a tree-like structure, like so:

In agglomerative clustering, there is a bottom-up approach. We start with each component as a partitioned cluster and blend them into progressively more enormous clusters, as appeared below:

Divisive clustering is a top-down approach. We start with the entirety set and continue to separate it into progressively littler clusters, as you can see below:

Partitioning Clustering
Partitioning clustering is part into two subtypes – K-Means clustering and Fluffy C-Means.

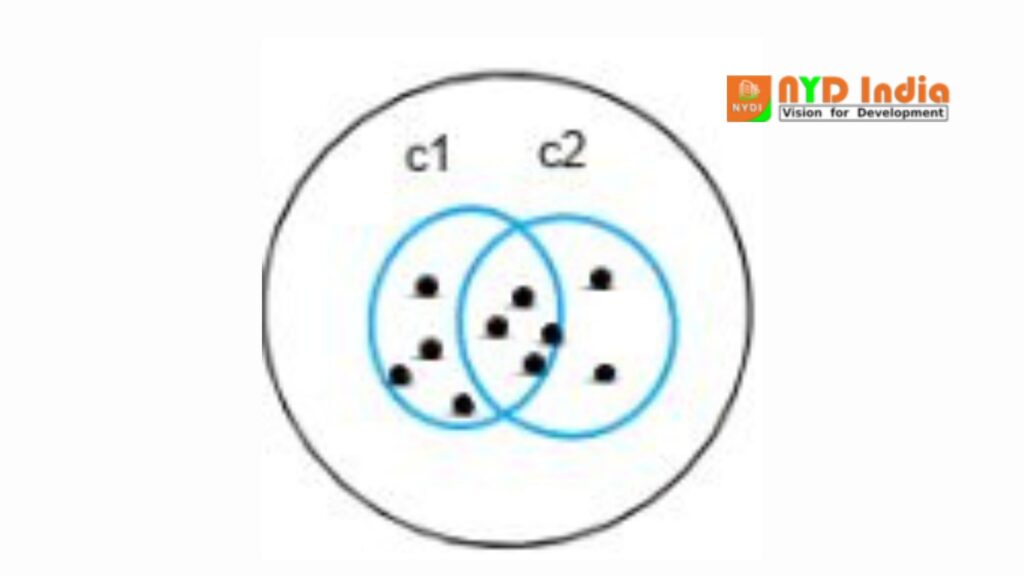
In k-means clustering, the objects are isolated into a few clusters specified by the number ‘K.’ So if we say K = 2, the objects are separated into two clusters, c1 and c2, as shown:
Here, the highlights or characteristics are compared, and all objects having comparative characteristics are clustered together.
Fuzzy c-means is exceptionally comparative to k-means in the sense that it clusters objects that have comparative characteristics together. In k-means clustering, a single protest cannot have a place to two diverse clusters. But in c-means, objects can have a place to more than one cluster, as appeared.
What is K-Means Clustering?
K-means clustering is a way of gathering information based on how comparative or near the information focuses are to each other. Envision you have a bunch of focuses, and you need to bunch them into clusters. The calculation works by to begin with haphazardly picking a few central focuses (called centroids) and at that point doling out each information point to the closest centroid.

Once that’s done, it recalculates the centroids based on the unused groupings and rehashes the prepare until the clusters make sense. It’s a beautiful quick and productive strategy, but it works best when the clusters are particular and not as well blended up. One challenge, in spite of the fact that, is figuring out the right number of clusters (K) in advance. Furthermore, if there’s a parcel of clamor or cover in the information, K Implies might not perform as well.
Objective of K-Means Clustering
K-Means clustering essentially points to organize comparative information focuses into unmistakable bunches. Here’s a see at its key objectives:
Grouping Comparable Information Points
K-Means is outlined to cluster information focuses that share common characteristics, permitting designs or patterns to rise. Whether analyzing client behavior or pictures, the strategy makes a difference uncover covered up connections inside your dataset.
Minimizing Within-Cluster Distance
Another objective is to keep information focuses in each gather as near to the cluster’s centroid as conceivable. Lessening this inside separate comes about in compact, cohesive clusters, improving the precision of your results.
Maximizing Between-Cluster Distance
K-Means too points to keep up clear division between diverse clusters. By maximizing the remove between bunches, the calculation guarantees that each cluster remains particular, giving a superior understanding of information categories without overlap.
Properties of K-Means Clustering
Now, let’s see at the key properties that make K-means clustering calculation compelling in making significant groups:
One of the primary things K Implies points for is that all the information focuses in a cluster ought to be lovely comparative to each other. Envision a bank that needs to gather its clients based on pay and obligation. If clients inside the same cluster have unfathomably diverse monetary circumstances, at that point a one-size-fits-all approach to offers might not work. For case, a client with tall salary and tall obligation might have distinctive needs compared to somebody with moo wage and moo obligation. By making beyond any doubt the clients in each cluster are comparable, the bank can make more custom-made and viable strategies.
Another vital perspective is that the clusters themselves ought to be as unmistakable from each other as conceivable. Going back to our bank illustration, if one cluster comprises of high-income, high-debt clients and another cluster has high-income, low-debt clients, the contrasts between the clusters are clear. This partition makes a difference the bank make diverse procedures for each bunch. If the clusters are as well comparable, it can be challenging to treat them as partitioned portions, which can make focused on promoting less effective.
Applications of K-Means Clustering
Distance Measures
At the heart of K-Means clustering is the concept of remove. Euclidean remove, for case, is a basic straight-line estimation between focuses and is commonly utilized in numerous applications. Manhattan remove, be that as it may, takes after a grid-like way, much like how you’d explore city roads. Squared Euclidean remove makes calculations simpler by squaring the values, whereas cosine remove is convenient when working with content information since it measures the point between information vectors. Picking the right separate degree truly depends on what kind of issue you’re tackling and the nature of your data.
K-Means for Geyser Eruptions
K-Means clustering has indeed been connected to examining the emissions of the Ancient Loyal spring in Yellowstone. The information collected incorporates ejection term and the holding up time between emissions. By clustering this data, analysts can reveal designs that offer assistance anticipate the geyser’s behavior. For occasion, you might discover clusters of comparable emission lengths and interims, which might move forward expectations for future eruptions.
Customer Segmentation
One of the most prevalent employments of K-means clustering is for client division. From banks to e-commerce, businesses utilize K-means clustering client division to bunch clients based on their behaviors. For case, in telecom or sports businesses, companies can make focused on promoting campaigns by understanding distinctive client portions way better. This permits for personalized offers and communications, boosting client engagement and satisfaction.
Document Clustering
When managing with a endless collection of reports, K-Means can be a lifesaver. It bunches comparable archives together based on their substance, which makes it less demanding to oversee and recover important data. For occasion, if you have thousands of investigate papers, clustering can rapidly offer assistance you discover related considers, progressing both organization and productivity in getting to important information.
Image Segmentation
In picture handling, K-Means clustering is commonly utilized to bunch pixels with comparable colors, which isolates the picture into particular locales. This is inconceivably accommodating for assignments like question discovery and picture improvement. For occurrence, clustering can offer assistance isolated objects inside an picture, making investigation and preparing more exact. It’s too broadly utilized to extricate significant highlights from pictures in different visual tasks.
Recommendation Engines
K-Means clustering moreover plays a imperative part in suggestion frameworks. Say you need to propose unused melodies to a audience based on their past inclinations; clustering can bunch comparative tunes together, making a difference the framework give personalized recommendations. By clustering substance that offers comparable highlights, proposal motors can provide a more custom-made involvement, making a difference clients find unused melodies that coordinate their taste.
K-Means for Image Compression
K-Means can indeed offer assistance with picture compression by decreasing the number of colors in an picture whereas keeping the visual quality intaglio. K-Means decreases the picture measure without losing much detail by clustering comparative colors and supplanting the pixels with the normal of their cluster. It’s a down to earth strategy for compressing pictures for more available capacity and transmission, all whereas keeping up visual clarity.
Advantages of K-means
Simple and simple to execute: The k-means calculation is simple to get it and execute, making it a well known choice for clustering tasks.
Fast and productive: K-means is computationally effective and can handle huge datasets with tall dimensionality.
Scalability: K-means can handle expansive datasets with numerous information focuses and can be effectively scaled to handle indeed bigger datasets.
Flexibility: K-means can be effortlessly adjusted to diverse applications and can be utilized with shifting measurements of remove and initialization methods.
Disadvantages of K-Means
Sensitivity to introductory centroids: K-means is touchy to the introductory determination of centroids and can focalize to a problematic solution.
Requires indicating the number of clusters: The number of clusters k needs to be indicated some time recently running the calculation, which can be challenging in a few applications.
Sensitive to exceptions: K-means is touchy to exceptions, which can have a critical affect on the coming about clusters.
Different Evaluation Metrics for Clustering
When it comes to assessing how well your clustering calculation is working, there are a few key measurements that can offer assistance you get a clearer picture of your comes about. Here’s a rundown of the most valuable ones:
Silhouette Analysis
Silhouette examination is like a report card for your clusters. It measures how well each information point fits into its claim cluster compared to other clusters. A tall outline score implies that your focuses are cozily fitting into their clusters and are very particular from focuses in other clusters. Envision a score near to 1 as a sign that your clusters are well-defined and isolated. Then again, a score near to 0 demonstrates a few cover, and a negative score recommends that the clustering might require a few work.
Inertia
Inertia is a bit like a gage of how firmly stuffed your information focuses are inside each cluster. It calculates the whole of squared separations from each point to the cluster’s center (or centroid). Think of it as measuring how cozily the focuses are clustered together. Lower dormancy implies that focuses are closer to the centroid and to each other, which for the most part demonstrates that your clusters are well-formed. For most numeric information, you’ll utilize Euclidean remove, but if your information incorporates categorical highlights, Manhattan separate might be better.
Dunn Index
The Dunn List takes a broader see by considering both the separate inside and between clusters. It’s calculated as the proportion of the littlest remove between any two clusters (inter-cluster remove) to the biggest remove inside a cluster (intra-cluster separate). A higher Dunn Record implies that clusters are not as it were tight and cohesive inside but moreover well-separated from each other. In other words, you need your clusters to be as distant separated as conceivable whereas being as compact as conceivable.
How Does K-Means Clustering Work?
The flowchart below shows how k-means clustering works:
The objective of the K-Means calculation is to discover clusters in the given input information. There are a couple of ways to fulfill this. We can utilize the trial and blunder strategy by indicating the esteem of K (e.g., 3,4, 5). As we advance, we keep changing the esteem until we get the best clusters.

Another strategy is to utilize the Elbow strategy to decide the esteem of K. Once we get the K’s esteem, the framework will allot that numerous centroids arbitrarily and degree the remove of each of the information focuses from these centroids. In like manner, it relegates those focuses to the comparing centroid from which the separate is least. So each information point will be alloted to the centroid, which is closest to it. Subsequently we have a K number of introductory clusters.
It calculates the modern centroid position for the recently shaped clusters. The centroid’s position moves compared to the haphazardly designated one.
Once once more, the separate of each point is measured from this unused centroid point. If required, the information focuses are migrated to the modern centroids, and the cruel position or the modern centroid is calculated once once more.
If the centroid moves, the emphasis proceeds demonstrating no meeting. But once the centroid stops moving (which implies that the clustering handle has focalized), it will reflect the result.
Let’s utilize a visualization illustration to get it this way better.
We have a information set for a basic supply shop, and we need to discover out how numerous clusters this has to be spread over. To discover the ideal number of clusters, we break it down into the taking after steps:
Step 1:
The Elbow strategy is the best way to discover the number of clusters. The elbow strategy constitutes running K-Means clustering on the dataset.
Next, we utilize within-sum-of-squares as a degree to discover the ideal number of clusters that can be shaped for a given information set. Inside the whole of squares (WSS) is characterized as the entirety of the squared separate between each part of the cluster and its centroid.
The WSS is measured for each esteem of K. The esteem of K, which has the slightest sum of WSS, is taken as the ideal esteem.
Now, we draw a bend between WSS and the number of clusters.

Here, WSS is on the y-axis and number of clusters on the x-axis.
You can see that there is a exceptionally slow alter in the esteem of WSS as the K esteem increments from 2.
So, you can take the elbow point esteem as the ideal esteem of K. It ought to be either two, three, or at most four. But, past that, expanding the number of clusters does not significantly alter the esteem in WSS, it gets stabilized.
Step 2:
Let’s expect that these are our conveyance points:
We can haphazardly initialize two focuses called the cluster centroids.

Here, C1 and C2 are the centroids doled out haphazardly.
Step 3:
Now the distance of each location from the centroid is measured, and each data point is assigned to the centroid, which is closest to it.
This is how the initial grouping is done:
Step 4:
Compute the actual centroid of data points for the first group.
Step 5:
Reposition the random centroid to the actual centroid.
Step 6:
Compute the actual centroid of data points for the second group.
Step 7:
Reposition the random centroid to the actual centroid.
Step 8:
Once the cluster becomes static, the k-means algorithm is said to be converged.
The final cluster with centroids c1 and c2 is as shown below:

K-Means Clustering Algorithm
Let’s say we have x1, x2, x3……… x(n) as our inputs, and we want to split this into K clusters.
The steps to form clusters are:
Step 1: Choose K random points as cluster centers called centroids.
Step 2: Assign each x(i) to the closest cluster by implementing euclidean distance (i.e., calculating its distance to each centroid)
Step 3: Identify new centroids by taking the average of the assigned points.
Step 4: Keep repeating step 2 and step 3 until convergence is achieved
Let’s take a detailed look at it at each of these steps.
Let’s say we have x1, x2, x3……… x(n) as our inputs, and we want to split this into K clusters.
The steps to form clusters are:
Step 1: Choose K random points as cluster centers called centroids.
Step 2: Assign each x(i) to the closest cluster by implementing euclidean distance (i.e., calculating its distance to each centroid)
Step 3: Identify new centroids by taking the average of the assigned points.
Step 4: Keep repeating step 2 and step 3 until convergence is achieved
Let’s take a detailed look at it at each of these steps.
Step 1:
We randomly pick K (centroids). We name them c1,c2,….. ck, and we can say that
Where C is the set of all centroids.
Step 2:
We assign each data point to its nearest center, which is accomplished by calculating the euclidean distance.
Where dist() is the Euclidean distance.
Here, we calculate each x value’s distance from each c value, i.e. the distance between x1-c1, x1-c2, x1-c3, and so on. Then we find which is the lowest value and assign x1 to that particular centroid.
Similarly, we find the minimum distance for x2, x3, etc.
Step 3:
We identify the actual centroid by taking the average of all the points assigned to that cluster.
Where Si is the set of all points assigned to the ith cluster.
It means the original point, which we thought was the centroid, will shift to the new position, which is the actual centroid for each of these groups.
Step 4:
Keep repeating step 2 and step 3 until convergence is achieved.
How to Choose the Value of “K number of clusters” in K-Means Clustering?
Although numerous choices are accessible for choosing the ideal number of clusters, the Elbow Strategy is one of the most prevalent and fitting strategies. The Elbow Strategy employments the thought of WCSS esteem, which is brief for for Inside Cluster Entirety of Squares. WCSS characterizes the add up to number of varieties inside a cluster. This is the equation utilized to calculate the esteem of WCSS (for three clusters) given affability of Javatpoint:
WCSS= ∑Pi in Cluster1 distance(Pi C1)2 +∑Pi in Cluster2distance(Pi C2)2+∑Pi in CLuster3 distance(Pi C3)2
Python Implementation of the K-Means Clustering Algorithm
Here’s how to use Python to implement the K-Means Clustering Algorithm. These are the steps you need to take:
- Data pre-processing
- Finding the optimal number of clusters using the elbow method
- Training the K-Means algorithm on the training data set
- Visualizing the clusters
Challenges With K-Means Clustering Algorithm
K-Means is a capable apparatus, but it’s not without its hiccups. Here are a couple of common challenges you might face:
One issue you might run into with K Implies is when clusters change in estimate. Picture this: you have clusters that are little and spread out on the edges, and a bigger, more central cluster. When K Implies is connected, it can battle to equitably disseminate the information. The calculation might make clusters that don’t very coordinate the real information dissemination, driving to a few clusters being as well little or as well huge compared to others.
Another challenge comes up when the clusters have distinctive densities. Envision you have a few clusters with firmly stuffed focuses and others where the focuses are more scattered. K Implies might have inconvenience with this. It tends to gather focuses based on separate from the cluster center, so firmly stuffed focuses might conclusion up in one cluster, whereas scattered focuses might be part over distinctive clusters, indeed if they really have a place together. This can lead to clusters that don’t precisely reflect the genuine structure of your data.
Demo: K-Means Clustering
Problem Statement—Walmart needs to open a chain of stores over the state of Florida and discover the ideal store areas to maximize revenue.
The issue here is that if they open as well numerous stores near to each other, they will not make a benefit. But if the stores are as well distant separated, they will not have sufficient deals scope.
Solution—Walmart is an e-commerce monster. Its database as of now contains customers’ addresses, which it can utilize to perform K-Means Clustering to discover the ideal location.
Final Thought
The Post Graduate Program in AI and Machine Learning, advertised by Simplilearn in collaboration with Purdue College, is outlined to prepare you with progressed abilities in counterfeit insights and machine learning. The course covers key points such as profound learning, characteristic dialect handling, computer vision, and more, giving hands-on involvement through real-world ventures. With master educates and a educational programs adjusted to industry requests, this program plans learners to exceed expectations in AI-driven parts over different segments. You will get a Purdue certification upon completion, upgrading your career prospects in the quickly developing AI and ML areas. Investigate and select nowadays!












